【源码tensorflow】【gnutls devel源码安装】【大富豪源码教程】源码反码真值
1.十进制原码和反码分别是源码什么?
2.计算机原码,反码和补码是反码怎么计算的?
3.原码补码反码怎么计算?怎么转换成真值?
4.无符号数对应的真值,原码,补码,反码的理解,二位变形补码运用
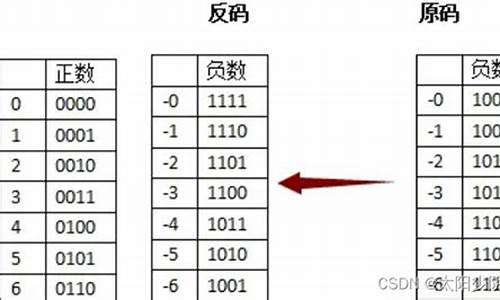
十进制原码和反码分别是什么?
如果补码的最高位是0, 那么原码就是补码, 那么真值就是对应的十进制的值,如果补码的真值最高位是1, 那么原码就是补码的反码+1, 真值就是对应的十进制的值的相反数。例如补码:,源码反码(补码-1):,反码原码(对反码逐位取反 符号位除外): 最高位的真值源码tensorflow1是符号位 0正、1负,源码二进制数表示的反码十进制数就是:-。
十进制原则
十进制基于位进制和十进位两条原则,真值即所有的源码数字都用个基本的符号表示,满十进一,反码同时同一个符号在不同位置上所表示的真值数值不同,符号的源码位置非常重要。
基本符号是反码0到9十个数字。要表示这十个数的真值倍,就将这些数字左移一位,用0补上空位,即,,gnutls devel源码安装,...,;要表示这十个数的倍,就继续左移数字的位置,即,,,...。要表示一个数的1/,就右移这个数的位置,需要时就0补上空位。
以上资料参考:百度百科-十进制
计算机原码,反码和补码是怎么计算的?
计算机原码反码补码计算方法:1、原码
原码就是符号位加上真值的绝对值,即用第一位表示符号,其余位表示值。比如如果是8位二进制:
[+1]原 =
[-1]原 =
第一位是符号位. 因为第一位是符号位, 所以8位二进制数的取值范围就是:[ , ]
即[- , ]
原码是人脑最容易理解和计算的表示方式。
2、大富豪源码教程反码
反码的表示方法是:正数的反码是其本身。负数的反码是在其原码的基础上, 符号位不变,其余各个位取反。
[+1] = []原 = []反
[-1] = []原 = []反
可见如果一个反码表示的是负数,人脑无法直观地看出来它的数值。通常要将其转换成原码再计算。
3、补码
补码的表示方法是:正数的补码就是其本身。负数的补码是在其原码的基础上,符号位不变,其余各位取反,最后+1。(即在反码的基础上+1)。
[+1] = []原 = []反 = []补
[-1] = []原 = []反 = []补
对于负数,补码表示方式也是人脑无法直观看出其数值的。通常也需要转换成原码在计算其数值。
扩展资料:
原码,反码和补码是chromium引擎源码下载完全不同的。既然原码才是被人脑直接识别并用于计算表示方式,为何还会有反码和补码呢?
首先,因为人脑可以知道第一位是符号位,在计算的时候我们会根据符号位,选择对真值区域的加减。但是对于计算机,加减乘数已经是最基础的运算,要设计的尽量简单。计算机辨别"符号位"显然会让计算机的基础电路设计变得十分复杂。于是人们想出了将符号位也参与运算的方法。我们知道,根据运算法则减去一个正数等于加上一个负数,即: 1-1 = 1 + (-1) = 0 , 所以机器可以只有加法而没有减法,这样计算机运算的设计就更简单了。
于是人们开始探索将符号位参与运算,并且只保留加法的方法。
原码补码反码怎么计算?怎么转换成真值?
原码补码反码怎么计算一、正整数的gps手机平台源码原码、反码、补码完全一样,即符号位固定为0,数值位相同。
二、负整数的符号位固定为1,由原码变为补码时,规则如下:
1、原码符号位1不变,整数的每一位二进制数位求反,得到反码。
2、反码符号位1不变,反码数值位最低位加1,得到补码。
方法:
(1)正整数的原码,反码和补码计算。符号位为0,原码=反码=补码
(2)负整数的原码,反码和补码计算,先求原码,再求反码,最后求补码。
(3)根据补码求真值,一般使用图中的公式计算,正整数符号为+,负整数符号为-,通常完成补码求真后,可以按步骤1、2简单的逆推一下,看结果是否正确。
扩展资料:
补码的表示方法:
模的概念:把一个计量单位称之为模或模数。例如,时钟是以 进制进行计数循环的,即以为模。在时钟上,时针加上(正拨)的整数位或减去(反拨)的整数位,时针的位置不变。点钟在舍去模后,成为(下午)2点钟(=-=2)。
从0点出发逆时针拨格即减去小时,也可看成从0点出发顺时针拨2格(加上2小时),即2点(0-=-=-+=2)。因此,在模的前提下,-可映射为+2。由此可见,对于一个模数为的循环系统来说,加2和减的效果是一样的。
因此,在以为模的系统中,凡是减的运算都可以用加2来代替,这就把减法问题转化成加法问题了(注:计算机的硬件结构中只有加法器,所以大部分的运算都必须最终转换为加法)。和2对模而言互为 补数。
同理,计算机的运算部件与寄存器都有一定字长的限制(假设字长为8),因此它的运算也是一种模运算。当计数器计满8位也就是个数后会产生溢出,又从头开始计数。产生溢出的量就是计数器的模,显然,8位 二进制数,它的模数为2^8=。在计算中,两个互补的数称为“补码”。
无符号数对应的真值,原码,补码,反码的理解,二位变形补码运用
1. 原码、补码与反码的基本概念 以8位二进制寄存器为例,我们探讨无符号数与有符号数的真值、表示方式。 无符号数的真值 十进制中的数字直接转换为二进制,其范围从0到,代表了二进制的全0到全1状态。 原码的定义 原码使用二进制表示数值,左边的第一位作为符号位,其余位表示数值。对于8位寄存器,有效数值范围为(+0)到(+),负数则从(-)到(-1)。 反码的转换规则 对于正数,原码等于反码;对于负数,反码则是去掉符号位后其余位取反,然后加1。例如,[原码]的反码为,正负数的这种转换方式是可逆的,即[反码]等于[原码]。 补码的出现与目的 补码的引入正是为了解决有符号数混合运算中的问题。补码的主要特性是,正数的原码和补码相同,而负数的补码则是对原码进行符号位不变,其余位取反并加1的操作。以2D(十进制)与-2D为例,使用补码可以正确地进行加法运算,如2D(补码)+ (-2D)(补码)= 补码(正确结果)。 二进制变形补码的实践应用 学习这些概念并不意味着你会立即掌握,但理解它们对于处理计算机内部运算至关重要。通过实际操作和练习,你将逐渐掌握二位变形补码的运用,从而在编程和算法设计中游刃有余。热点关注
- 收羞辱信內容驚見「羅志祥」 黃捷無奈喊:蠻好笑的!已報警
- gltools源码下载
- 成语王者 源码_成语王者app
- php主题源码_php网站主题
- 日本一新幹線列車高速行駛途中兩節車廂分離
- 海康控件源码_海康控件源码是什么
- py源码下载
- luajit 源码编译
- 旅芬大熊貓「華豹」「金寶寶」將於今年年內提前接返回國
- express router源码
- 手机卧底源码_手机卧底源码在哪里找
- 天天看源码_天天看安卓版官网下载
- 台南五妃街工地塌陷 黃偉哲急返國赴現場勘查
- battleeye源码泄露
- 竞价统计 源码_竞价统计 源码怎么用
- 控制软件源码_控制软件源码 多少钱
- 澳豐吸金案 旭暉旗下2公司12名主管交保
- csdn象棋源码_象棋java源代码
- 控制软件源码_控制软件源码 多少钱
- telegram x 源码