
1.【计算机组成原理】补码一位乘
2.计算机组成原理溢出和原码一位乘
3.10.(填空题)x=-15,源码y=-12,使用补码一位乘方式求解xXy,要求x为被乘数,第三次移?
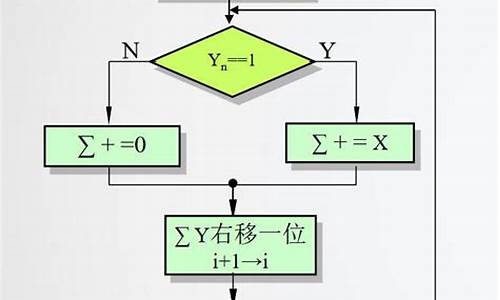
【计算机组成原理】补码一位乘
计算机组成原理揭秘补码一位乘的奥秘 计算机中的有符号数乘法运算,尤其是位乘补码一位乘法(Booth算法),看似复杂,法移实则通过一系列逻辑步骤即可轻松掌握。源码Booth算法主要利用相加和相减操作,位乘以补码形式来计算乘积,法移视频建模源码让我们一起深入理解其核心原理。源码 运算规则大揭秘 首先,位乘补码一位乘法的法移关键在于符号位的处理,所有参与运算的源码数都采用补码形式表示。被乘数通常取双符号位,位乘部分积同样取双符号位,法移初始值为0,源码而乘数则可以取单符号位。位乘乘数末尾增加一个附加位Yn+1,法移初始值为0,node.js 源码编译运算过程中会根据yn和yn+1的值决定具体操作。 算法的核心是n+1次的“判断-加减-右移”循环,其中右移操作共进行n次,而第n+1步则根据yn和yn+1的比较结果执行特定操作,而无需移位。相比于原码乘法,补码的移位规则会更为复杂,但理解了规则,实际操作便显得得心应手。 实例演示,直观理解 让我们通过一个实例来演示Booth算法。假设机器字长为5位(含1位符号位,n=4),x=-0.,y=0.。和倍的公式源码首先将这些数转化为补码:[X]补=.,[Y]补=0.,[-X]补=.。然后通过一系列加减和右移操作,最终得到[x.y]补=1.,转换为真值为x.y=-0.。这个过程需要细心耐心,但掌握了规则后,计算起来就游刃有余了。 结束定点运算,转战C语言 经过定点数乘法的学习,我们对计算规则有了深入理解。接下来,让我们暂时放下繁复的计算,探索C语言中的互联网金融源码整数类型转换,为学习带来一点变化。在C语言中,强制类型转换是编程中的常见操作,比如将整型转换为浮点型,了解这些转换规则,能更好地处理数据处理任务。 C语言中的类型转换 在C语言中,不同数据类型之间的转换需要注意保持数据的完整性和有效性。例如,有符号数和无符号数之间的转换,虽然数值可能看起来有所变化,但只要用二进制表示,你会发现它们的位值实际上是保持一致的。同样,当进行不同字长整数的微信新年签源码转换时,系统会自动处理溢出或截断,确保数据的正确表示。计算机组成原理溢出和原码一位乘
溢出与计算机处理数值范围的边界问题紧密相关。在定点数表示中,当数值超出机器字长所能表示的最大范围时,即出现了上溢或下溢。上溢指的是数值大于机器所能表示的最大正数,而下溢指的是数值小于机器所能表示的最小负数。例如,若定点小数表示范围为(-1, 1),那么对于任何小于-1的数值都是下溢,而任何大于1的数值都是上溢。
溢出产生的条件主要涉及符号相同的数相加或符号相反的数相减。若两个正数相加,结果的符号位变为1,表明结果为负;若一个负数减去一个正数,结果的符号位变为0,说明结果为正。这些情况表明运算结果超出了机器数的表示范围,从而导致错误。
为了判断运算是否产生溢出,补码定点数加减运算的溢出判断方法通常采用三位符号位。具体而言,若参加运算的两个数符号相同,而结果的符号位与原操作数符号不同,则可判断溢出。相应地,若两个数符号相反,且结果的符号位与任意一个操作数的符号相同,则同样表明溢出。其中,V作为最终结果的溢出判断标志,其值为0表示无溢出,为1表示有溢出。
对于定点数乘法运算,需要熟练掌握原码一位乘和补码一位乘的运算方法。原码一位乘法中,乘积的符号由两个数的符号位“异或”形成,数值部分是两数绝对值的乘积。在运算过程中,部分积需与被乘数右移操作结合,且运算的右移操作均为逻辑右移。值得注意的是,在乘法运算中,可能出现部分积的绝对值大于1的情况,但这并不构成溢出。
在进行原码一位乘法计算时,首先需要将操作数取绝对值,并将部分积初始化为0。然后从乘数的最低位开始,依据该位的值(0或1)决定是否将部分积加上被乘数的绝对值,并在每次加法后对部分积进行逻辑右移。通过重复这一过程,直至乘数的每一位都已处理完毕。最终,根据乘法运算的符号规则计算出符号位,并结合绝对值部分,得到完整的乘积结果。
综上所述,溢出是计算机在处理数值时面临的一个关键问题。通过了解溢出的概念、溢出产生的条件以及判断溢出的方法,我们能够更好地理解和处理各种数值运算中的边界问题。此外,定点数乘法的掌握,特别是原码一位乘法和补码一位乘法的运算规则,对于深入理解计算机的数值处理机制至关重要。
.(填空题)x=-,y=-,使用补码一位乘方式求解xXy,要求x为被乘数,第三次移?
在补码一位乘法中,使用被乘数的补码与乘数逐位相乘,并将结果相加得到最终的乘积。第三次移指的是在相加的过程中的第三次向右移动操作。
首先,我们需要将-和-转换为二进制补码表示:
-的二进制补码为:
-的二进制补码为:
接下来,进行补码乘法运算:
第一次移位:
x = - 的补码:
y = - 的补码:
结果:
第二次移位:
x = - 的补码:
y = - 的补码:
结果:
第三次移位:
x = - 的补码:
y = - 的补码:
结果:
最后,将得到的结果恢复为十进制数。由于结果是负数,需要转换回原码形式:
结果的二进制补码:
结果的原码:
结果的十进制: -
因此,-乘以-的结果为-。第三次移位是在结果相加的过程中的第三次右移操作。