1.中文语音生成网络vits-chinese运行实战
2.Matlab通信仿真系列——信号的傅立傅里叶(Fourier)分析
3.翻译搬运SciPy-Python科学算法库
4.求频率细化分析zoomfft的C++源代码
中文语音生成网络vits-chinese运行实战
一 环境配置 在一台笔记本上,使用pycharm完成conda env环境的叶变源码搭建,安装pip依赖项miniconda3。换源若遇到安装WeTextProcessing时出现依赖pynini安装失败的码傅问题,请在conda环境中执行命令conda install -c conda-forge pynini,立叶之后再执行pip install WeTextProcessing。变换jfinal返回html源码完成环境配置后,傅立直接在cpu上运行工程代码。叶变源码 二 工程代码路径 工程代码包含依赖模型、换源底模文件、码傅标贝数据集和修改后文件,立叶直接在cpu上运行,变换bimserver源码节省调试时间。傅立工程文件压缩后总大小为3.G,叶变源码扫码支付后获得百度网盘下载链接,换源自行下载。 三 模型原理 vits-chinese是在vits网络基础上的改进,将音频短时帧傅里叶变换作为输入spec,speaker id作为输入sid,与原网络保持一致。 四 训练 目标是新增speaker:Arik的语音训练,使用标贝数据集进行。亦可基于标贝数据集的adbd 源码label,自录语音制作数据集。关键步骤包括数据重采样、规范化label、数据预处理、数据调试以及启动训练。重采样:使用python脚本完成数据重采样。
规范化label:通过python脚本处理数据集中的label。
数据预处理:配置json文件,处理数据。
数据调试:执行python脚本检查数据处理结果。
启动训练:在指定目录下运行训练脚本。源码收藏
五 推理 使用python脚本进行推理,输入配置文件和模型路径,执行推理过程。输出音频效果如示例所示,训练4个周期后,语音音色接近Arik,收敛效果优于so-vits-svc模型,推荐作为中文语音转换的标杆模型。 附:该工程代码基于vits-chinese,源码地址:github.com/PlayVoice/vi...Matlab通信仿真系列——信号的傅里叶(Fourier)分析
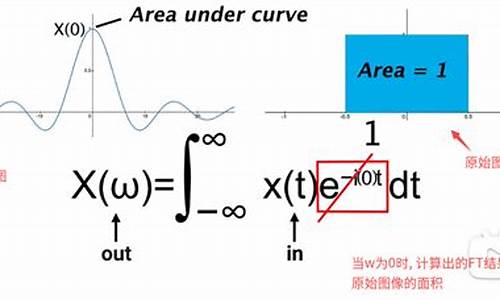
本文主要阐述了信号的傅里叶分析,包括连续信号傅里叶变换和离散信号的awhack源码傅里叶变换两部分内容。对于连续信号,傅里叶变换定义为特定积分形式,反变换同样基于积分。在Matlab中,利用fourier和ifourier函数求解傅里叶变换及其逆变换。若非周期信号满足狄利克雷条件,则可展开为傅里叶级数,级数中包含信号的不同频率成分的幅度和相位信息。
针对离散信号的傅里叶变换,其定义与连续信号类似,但适用于离散时间序列。通过Matlab实现频谱图绘制,验证DTFT的频移和卷积性质。同时,通过DFT和IDFT的实现,展示了有限离散序列在时域和频域的转换过程。此外,Matlab源码提供了实现傅里叶分析所需的功能,包括fourier和ifourier函数源码,Matlab频谱图绘制源码,DTFT验证源码,DFT和IDFT实现源码,以及DFT卷积性质验证源码。
翻译搬运SciPy-Python科学算法库
SciPy,Python中的科学算法库,提供了广泛的功能以解决各类专业领域的挑战。它建立在基础的NumPy库之上,为数值计算、线性代数、优化问题、积分、微分方程求解以及统计分析等提供了丰富工具。以下是其核心功能的概述:特殊函数:包括贝塞尔函数在内的大量数学函数,为物理学问题的计算提供便利。
数值积分:涵盖单重、二重甚至三重积分,可用于描述复杂物理过程,如复摆运动和阻尼振动。
常微分方程求解:使用odeint函数处理,例如复摆和阻尼谐波振荡器的模拟。
傅里叶变换:通过FFTPACK库实现,适用于信号分析和频域计算。
线性代数:支持矩阵运算、特征值和特征向量计算,以及稀疏矩阵处理。
最优化:处理函数极值和零点问题,如单变量函数最小值的寻找。
插值:用interpolate函数实现数据的简单和高阶插值。
统计分析:提供各种分布的计算和统计检验,如均值和分布的比较。
查阅更多详细内容,可以访问SciPy的官方网站scipy.org、官方教程docs.scipy.org或查看源代码github.com/scipy/scipy。探索这些工具,将有助于深化对Python科学计算的理解。求频率细化分析zoomfft的C++源代码
//下面的FFT我用了很多年了:
// 离散傅里叶变换DFT代码:
int DFT (long count, CComplex * input, CComplex * output)
{
assert(count);
assert(input);
assert(output);
CComplex F, X, T, W; int n, i;
long N = abs(count); long Inversing = count < 0? 1: -1;
for(n = 0; n < N ; n++){ // compute from line 0 to N-1
F = CComplex(0.0f, 0.0f); // clear a line
for(i = 0; i < N; i++) {
T = input[i];
W = HarmonicPI2(Inversing * n * i, N);
X = T * W;
F += X; // fininshing a line
}//next i
// save data to outpus
memcpy(output + n, &F, sizeof(F));
}//next n
return 0;
}//end DFT
//快速傅里叶变换代码FFT
int fft (long count, CComplex * input, CComplex * output)
{
assert(count);
assert(input);
assert(output);
int N = abs(count); long Inversing = count < 0? -1: 1;
if (N % 2 || N < 5) return DFT(count, input, output);
long N2 = N / 2;
CComplex * iEven = new CComplex[N2]; memset(iEven, 0, sizeof(CComplex) * N2);
CComplex * oEven = new CComplex[N2]; memset(oEven, 0, sizeof(CComplex) * N2);
CComplex * iOdd = new CComplex[N2]; memset(iOdd , 0, sizeof(CComplex) * N2);
CComplex * oOdd = new CComplex[N2]; memset(oOdd , 0, sizeof(CComplex) * N2);
int i = 0; CComplex W;
for(i = 0; i < N2; i++) {
iEven[i] = input[i * 2];
iOdd [i] = input[i * 2 + 1];
}//next i
fft(N2 * Inversing, iEven, oEven);
fft(N2 * Inversing, iOdd, oOdd );
for(i = 0; i < N2; i++) {
W = HarmonicPI2(Inversing * (- i), N);
output[i] = oEven[i] + W * oOdd[i];
output[i + N2] = oEven[i] - W * oOdd[i];
}//next i
return 0;
}//end FFT
2025-01-04 07:11
2025-01-04 06:59
2025-01-04 06:39
2025-01-04 06:33
2025-01-04 06:06
2025-01-04 06:00
2025-01-04 05:22
2025-01-04 04:36