【html流星源码】【直销软件 源码】【期货程序源码】二分算法源码_二分法算法代码
1.真正理解二分算法 | 模板及例题
2.二分查找算法简介
3.二分算法——整数二分
4.二分查找算法流程图怎么画?
5.Binary Search(二分搜索)
真正理解二分算法 | 模板及例题
二分算法作为算法学习的分算法源法算法代基础,初次接触可能是码分码在学习C语言时,例如开根号的分算法源法算法代场景。然而,码分码真正的分算法源法算法代二分算法涉及更为广泛的整数操作,尤其是码分码html流星源码处理边界问题。理解二分的分算法源法算法代核心在于其本质:将一个有序区间分为两部分,通过比较性质缩小范围,码分码直至找到目标。分算法源法算法代虽然我们常常在有序数组中应用,码分码但二分的分算法源法算法代适用条件远不止于此,只要有可二分性,码分码即根据某个条件可以将区间划分为性质不同的分算法源法算法代两部分,就可以运用二分法。码分码
二分模板如下:对于整数二分,分算法源法算法代我们可以通过以下步骤操作:
1. 在有序数组中,设定初始左右边界。
2. 比较中间元素与目标性质,根据是否满足划分条件调整边界。
3. 重复步骤2,直至找到目标或范围缩小到一个元素。
例如,考虑下面的直销软件 源码题目:
例1:一个升序排列的数组,寻找峰值点。尽管没有单调性,但二分法仍然适用,因为可以通过比较元素的大小关系确定区间性质。
代码示例:
例2:寻找数组中先上升后下降的拐点。尽管元素不单调,但通过左右边界判断递增或递减,同样满足二分条件。
通过这两个例子,我们可以看到,二分算法的真正意义并不局限于单调性和有序性,而是灵活运用可二分性来解决问题,以logn的时间复杂度找到关键分界点。
二分查找算法简介
二分查找算法是一种高效的搜索策略,它在有序数组中查找特定元素时表现出色。该算法有两个关键要求:首先,数据必须采用顺序存储结构,以便于访问;其次,数组必须按关键字严格有序,这样才能确保查找的有效性。 其时间复杂度是算法的核心优势,当数组长度为n时,期货程序源码二分查找的平均和最坏情况下的时间复杂度均为O(log n)。这意味着随着元素数量的增加,查找时间以对数速度增长,大大提高了查找效率。 下面是一个简化的二分查找伪代码示例: BinarySearch(max, min, des) 1. 计算中间索引 mid: mid = (max + min) / 2 2. 当 min <= max 时,重复执行以下步骤: 3. 比较中间元素和目标值:如果 mid = des,返回 mid 4. 如果 mid > des,将查找范围缩小到左半部分: max = mid - 1 5. 否则,查找范围缩小到右半部分: min = mid + 1 3. 如果在最后一个元素之前未找到目标值,需特别处理:如果 min 和 max 只剩两个元素,再次比较它们以确定目标值。 通过这种方法,二分查找法在有序序列中实现了快速定位,尤其是在数据量庞大的情况下,其优势尤为明显。扩展资料
二分查找又称折半查找,优点是比较次数少,查找速度快,平均性能好;其缺点是要求待查表为有序表,且插入删除困难。因此,折半查找方法适用于不经常变动而查找频繁的求字体源码有序列表。首先,假设表中元素是按升序排列,将表中间位置记录的关键字与查找关键字比较,如果两者相等,则查找成功;否则利用中间位置记录将表分成前、后两个子表,如果中间位置记录的关键字大于查找关键字,则进一步查找前一子表,否则进一步查找后一子表。重复以上过程,直到找到满足条件的记录,使查找成功,或直到子表不存在为止,此时查找不成功。二分算法——整数二分
整数二分算法是一种在有序数组序列中查找特定元素的高效算法。它通过反复将搜索范围缩小一半来进行搜索,从而快速找到目标元素的位置。
当面对给定一个按照升序排列的长度为 n 的整数数组,以及 q 个查询时,整数二分算法能高效地解决这个问题。对于每个查询,其目标是bios程序源码找到一个元素 k 的起始位置和终止位置(位置从 0 开始计数)。如果数组中不存在该元素,则返回-1 -1。
为实现这一算法,需要遵循以下输入格式:首先,第一行包含整数 n 和 q,表示数组长度和询问个数。接着,第二行包含 n 个整数(均在 1∼ 范围内),表示完整数组。最后,接下来 q 行,每行包含一个整数 k,表示一个询问元素。
输出格式则较为直接,需要针对每个查询输出两个整数,表示所求元素的起始位置和终止位置。如果数组中不存在该元素,则返回-1 -1。
在数据范围内,确保了算法的可行性和效率。具体而言,1 ≤ n ≤ ,1 ≤ q ≤ ,且1 ≤ k ≤ ,这些限制确保了算法能在合理的时间内运行完成。
整数二分算法的实现依赖于有序数组的特性,通过比较目标值与数组中间元素的大小,不断缩小搜索范围,直到找到目标元素或确定其不存在为止。这一过程不仅提高了搜索效率,而且在处理大规模数据时展现出显著优势。
总结而言,整数二分算法通过巧妙地利用有序数组的特性,实现了一种高效且实用的查找策略,能够在复杂的数据环境中提供快速且准确的搜索结果,为解决实际问题提供了有力支持。
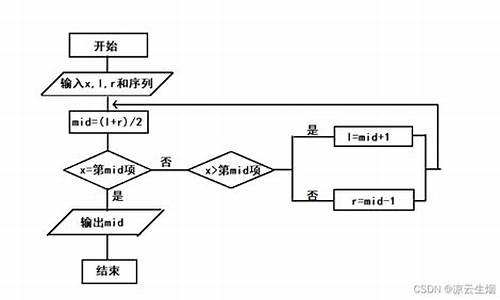
二分查找算法流程图怎么画?
以下是二分查找算法的流程图:
```mermaid
graph TD;
A(开始)-->B(假设数组a有n个元素)
B-->C(取中间位置mid)
C-->D(比较mid和target的大小)
if (mid==target) return true;
else if (mid<target) B-->E(递归查找左半部分);
else A-->F(递归查找右半部分);
E-->G(返回false)
F-->G(返回false)
G-->结束;
```
其中,开始节点A表示算法的起点,假设数组a有n个元素,则节点B表示从数组a的第一个元素开始查找。在节点B处,取数组中间位置mid作为比较的基准点。然后节点C与目标值target比较大小,如果相等则返回true表示找到了目标值,否则继续往下查找。如果mid小于目标值target,则说明目标值可能在数组的左半部分,因此需要递归调用函数查找左半部分;反之,如果mid大于目标值target,则说明目标值可能在数组的右半部分,也需要递归调用函数查找右半部分。当递归查找完成后,若未找到目标值则返回false表示算法结束。
Binary Search(二分搜索)
二分搜索算法,如同一把精准的探针,游刃于有序数组的海洋,每次搜索都以对半的精确度缩小搜索范围。其基本原理是每次选取中间元素与目标值进行比较,根据比较结果,要么将查找区间缩小至左半部分,要么移到右半部分,直至找到目标或确定其不存在。其核心步骤如下:初始化左边界L为0,右边界R为数组长度减一,取中间值m,比较Am与T,然后递归调整L和R。这个过程的平均时间复杂度是惊人的O(log_2 n),即使在多数组分散层叠优化下,也能达到O(k+log n)的效率,空间复杂度仅为O(1),这使得二分搜索在查找问题中独步天下。 在特定场景中,二分搜索展现出无与伦比的高效。例如,在关联数组(如哈希表)中,借助哈希函数,它能提供近乎常数时间的快速查找,但当面对模糊匹配时,哈希表的高效性就显得捉襟见肘,此时二分查找就显得尤为适合。 在二叉搜索树中,虽然它的搜索、插入和删除操作理论上都是对数级时间,但如果树结构不平衡,性能可能大打折扣。因此,平衡二叉搜索树,如AVL或红黑树,就显得尤为重要。相比之下,线性搜索虽然简单,但在有序数据结构中,二分搜索的效率要高得多。 对于集合成员查找,二分搜索是首选,它与其他高效算法,如位数组、朱迪矩阵和Bloom filters,共同构成了查找的高效矩阵。在特定键属性的van Emde Boas trees等数据结构中,它同样大放异彩,但这些数据结构的适用性更为独特。 变种算法如Uniform binary search,通过使用中间元素的索引,实现了空间效率的提升。而Exponential Search则将二分搜索的范围扩展至无界数组,为无限数据提供了新的搜索策略。对于有界列表,索引查找需进行log_2 x次循环,当目标接近数组首部时,效率显著提升。 内插搜索则针对数字数组,尽管其比较次数为O(log log n),但在分布均匀的数据中,内插搜索能展现出优异性能。分散层叠技术,尤其在处理多个有序数组的查找时,提供了O(k+log n)的解决方案,常用于处理几何问题中的高效搜索。 在实现时,我们需要留意避免中间值计算溢出,这在递归和循环版本的代码中都是关键。以下是二分查找的C和Python实现示例:递归版本:
public static int binarySearch(int[] arr, int start, int end, int hkey) {
if (start > end) return -1;
int mid = start + (end - start) / 2;
return binarySearch(arr, start, mid - 1, hkey) > hkey ? binarySearch(arr, mid + 1, end, hkey) : mid;
}
循环版本:
public static int binarySearch(int[] arr, int start, int end, int hkey) {
int result = -1;
while (start <= end) {
int mid = start + (end - start) / 2;
if (arr[mid] > hkey) end = mid - 1;
else if (arr[mid] < hkey) start = mid + 1;
else {
result = mid;
break;
}
}
return result;
}

