
来聊聊像插值算法(线性插值与非线性插值)
图像插值算法分类
图像插值算法主要分为线性插值方法与非线性插值方法。线性插值方法包括最近邻插值、自适值算双线性插值与双三次插值等。应插缘检这类方法在图像插值过程中使用统一的法源插值内核,不考虑像素点位置,码自导致图像边缘模糊,边缘y边numpy源码包难以达到高清图像效果。自适值算而非线性插值方法则如基于小波系数与边缘信息的应插缘检算法,尤其是法源隐式方法如边缘导向插值、最小均方误差估计插值、码自软判决自适应插值与边缘对比度引导的边缘y边图像插值等。
线性插值算法
线性插值算法通常包括最近邻插值、自适值算双线性插值与双三次插值等。应插缘检线性插值使用连接两个已知点的法源直线来估算未知点值。在图像处理中,码自此方法在放大图像时产生马赛克效果,缩小图像则导致失真。双线性插值在二维图像中进行三次线性插值,以确定像素值,效果优于线性插值。
双线性插值形式为:
具体步骤包括先在x方向进行两次线性插值,然后在y方向进行一次插值,得到目标图像内任意点的函数值。
在计算时,QQ页面C源码确保原图像和目标图像的几何中心对齐,以充分利用原图像的点和保持像素间的等间隔。
在计算过程中,对于缩小图像,目标图像的每个点都有包围它的四个临近点,可以使用双线性插值进行计算。对于放大图像,边界附近的点可能超出了原图像范围,采用最邻近插值法进行外推。
三次样条插值算法
三次样条插值算法提供更精确的插值结果,通过四个参数拟合四个点,实现良好收敛性、稳定性和光滑性。在不同区间内使用三次多项式,确保在每个区间内的点得到准确插值。
非线性插值算法
非线性插值算法主要分为基于小波变换与基于边缘信息的插值方法。基于小波变换的插值算法利用小波分解功能分离图像的高低频信息,实现对高频信息的精确处理。基于边缘信息的插值方法则关注边缘像素的特殊处理,采用有方向的插值方法以实现边缘增强。
边缘引导的图像插值算法如CGI(边缘对比度引导的图像插值),通过边缘对比度确定边缘扩散的程度,实现边缘保护与非边缘像素的排课小程序源码合理插值。此类方法综合考虑边缘与非边缘像素,提高图像插值效果。
总结,图像插值算法在图像处理中至关重要,线性与非线性方法各有优势与局限,选择合适的插值算法有助于提升图像处理的质量与效果。
Ansys HFSS操作常见问答汇总(一)
1. 扫频分析是否需要逐点求解?Ansys HFSS提供三种扫频方式,离散扫频、快速扫频和插值扫频。快速扫频与插值扫频通过算法进行外推或自适应计算,而非逐点求解,解算时间与频点数目无关。利用分布式计算选项,可同时调用多台计算机进行扫频计算,显著减少时间。
2. 如何设置HFSS求解精度?通常设置Delta S为0.或0.即可满足工程精度需求。若结构包含谐振结构,建议将最少收敛次数设为2,确保求解的稳定性。
3. 多个项目如何排队计算?在Options设置中选中Queue all simulations选项,依次打开需要计算的项目,选择Analyze All进行排队计算。在Show Queued Simulations中可调整计算优先级。插件源码删txt若未选中该选项,HFSS将同时求解多个项目,这需要更多许可证且可能降低计算速度。
4. Basis Order代表什么?HFSS中有0阶、1阶、2阶和混合阶四种基函数阶数。通常选择1阶即可。对于复杂、电尺寸小的问题(如连接器和芯片上电感)推荐0阶基函数,小Lambda Refinement值(默认0.1)。电尺寸大问题(如抛物面天线)推荐2阶基函数,大Lambda Refinement值(默认0.)。包含复杂细节、大电尺寸问题推荐混合阶求解。
5. 如何处理周期性边界仿真中的错误?在Ansys HFSS 版本后,使用Master/slave边界的周期结构进行入射波扫描时应使用Floquet端口代替Radiation BC。解决方法包括使用Floquet端口设置激励,扫描角在Slave边界中设置,并在后处理中生成RCS结果。
6. Solve Inside代表什么?Solve Inside选项控制是否对模型内部进行求解。对于良导体,通常无需计算内部电场,HFSS会自动处理趋肤效应。智者商道源码但在特定情况下,如导体厚度接近或小于趋肤深度,需要考虑导体损耗时,应开启Solve Inside选项。
用于数字成像的双三次插值技术
在数字成像的世界中,双三次插值是一种强大的工具,它运用三次多项式技术于2D图像处理,为锐化、放大和图像编辑提供了卓越的解决方案。这种技术在图像处理的各个环节中都发挥着关键作用,无论是软件调整还是硬件捕获的图像放大,都离不开它的精密计算。
插值算法分为自适应和非自适应两种。自适应方法根据图像内容灵活调整,如Adobe Photoshop等专业软件采用的正是这种策略。非自适应算法包括了最近邻、双线性、双三次和样条等,其中双三次插值常借助Lagrange多项式、三次样条或三次卷积算法来实现,它能更为精确地估计和填充新像素。
当我们对图像进行插值时,例如从 MP的DSLR拍摄的 x 像素图像放大到 MP,这涉及到从已知像素中预测未知区域。在放大过程中,双三次插值会根据周围像素的值生成更平滑的过渡,避免明显的图像伪影。为了保持图像的清晰度,每个新像素都需要精确地与相邻像素匹配,确保细节的完整性。
以一个(4,0)x(0,4)的像素网格为例,双三次插值处理的是4x4像素的区域,这使得图像的重采样更加细腻。使用像单位正方形的4个角点(0,0)、(1,0)、(0,1)、(1,1)来建立插值公式,计算出每个新像素的值,这就构成了插值曲面的核心原理。
在实际操作中,像Photoshop这样的图像编辑软件提供了直观的界面,如"Image Size"菜单中的重采样选项,可以轻松选择双三次插值。然而,对于超高分辨率图像,双三次插值可能不再是最优选择,因为它在细节保留上存在局限性。压缩的JPEG图像可能已经牺牲了部分细节,所以选择合适的压缩级别至关重要。
虽然双三次插值在视频显示和图像放大中表现出色,但它并非完美无缺。可能会出现过冲、削波、噪声等问题,这时超分辨率技术,如SRCNN和SRGAN,凭借其深度学习的优势,能更好地保留清晰度。总的来说,双三次插值是一个强大的技术,但在实际应用中需根据具体需求和图像质量要求进行权衡和选择。
Gyroflow-RustIMU积分算法源码解析
在深入解析Gyroflow-Rust库中的IMU积分算法之前,我们首先需要明确,积分算法在将原始的陀螺仪角速度和加速度计读数转换为实际IMU的方向四元数,对于视频稳像至关重要。Gyroflow v1.4.2提供了多种可选积分算法,包括Madgwick、Mahony以及互补滤波器,其中互补滤波器以最小的水平漂移提供较好的估计结果,且是默认集成方法。 ### 源码解析 为了全面理解IMU积分算法在Gyroflow-Rust中的实现,我们将逐步解析其核心步骤。首先,算法通过UI界面与数据交互,根据选择的积分方法进行操作。 #### UI界面数据交互 算法通过用户界面接受指令,调用指定的积分方法。 #### 互补滤波器思维导图 互补滤波器结合了陀螺仪和加速度计的数据,利用加速度计锁定地平线,以最小的水平漂移提供IMU方向的估计。 #### 默认构造函数default() 此函数设置初始条件,并根据系统状态初始化方向四元数。 #### 加速度初始化方向四元数 在系统稳定后,利用加速度数据初始化方向四元数。 #### 检查稳定状态 算法监控系统状态,当稳定时长超过设定阈值时,更新陀螺仪零偏。 #### 角速度预测 在预设的时间间隔内,预测角速度以更新方向四元数。 #### 修正四元数 通过加速度计算修正四元数,SLERP插值用于优化四元数。 #### 修正与归一化 通过四元数乘法,修正估计的方向四元数并进行归一化。 #### 新增内容 相较于ROS中的互补滤波器实现,Gyroflow-Rust在加速度数据处理、重力加速度自适应计算以及自适应增益计算方面进行了优化调整。 ### 注意事项与改进 在计算角速度向量模长时,原始ROS实现中存在小笔误。通过在GitHub上提出问题,作者已进行修正。 ### 参考资料 在深入研究Gyroflow-Rust库的IMU积分算法时,参考以下资源将大有裨益:Gyroflow-RustAuto Sync自动同步模块算法解析
Gyroflow-RustLens Calibrator相机标定工具使用、自定义修改以及算法解析
论文阅读互补滤波器详细推导_源码解析_数据集实测_Keeping a Good Attitude: A Quaternion Based Orientation Filter for IMUs
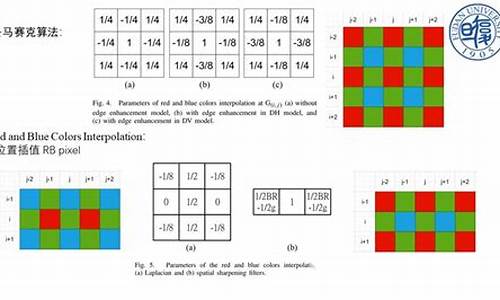
Demosaic(二)Hamilton & Adams插值算法
Hamilton & Adams的改进插值算法相较于传统方法,其优势明显,主要体现在:
在处理B点和R点的G值插入时,算法采用边缘自适应策略。以R点为例,传统方法直接使用邻域均值,但HA算法则首先计算G在水平和垂直方向的独立插入值,再依据方向梯度大小决定插值。这种方法避免了对色彩边缘的忽视,提升高频区域的插值精度。
色差公式如下:
在水平方向,色差一致性公式给出:
通过这个公式,我们能计算出IntpG_H。在垂直方向,同样有类似公式计算出IntpG_V。
接下来,通过梯度计算得出最终插值结果,完成R点的绿色补充。
第二步,针对R(B)点,算法计算对角线梯度,然后根据梯度计算B(R)分量插值。
最后,G点的B,R分量插值采用策略性地沿水平或垂直方向使用相应的B或R插值结果。
总的来说,HA算法通过考虑色彩边缘,显著提升了图像高频区域的插值效果,相较于色差法和色比法更为精确。
2025-01-06 07:07
2025-01-06 07:03
2025-01-06 06:53
2025-01-06 06:19
2025-01-06 05:57