1.Androidåºç¡ãV1V2V3ç¾åã
2.79C3125EAC1CE25EE2C99A9B01DFC00
3.nmap的指纹源码其他实战应用
4.Matlab指纹识别详细解析 参考源码
Androidåºç¡ãV1V2V3ç¾åã
åºç¡æ¦å¿µç¾åï¼å¨ APK ä¸åå ¥ä¸ä¸ªãæ纹ããæ纹åå ¥ä»¥åï¼APK ä¸æä»»ä½ä¿®æ¹ï¼é½ä¼å¯¼è´è¿ä¸ªæ纹æ æï¼Android ç³»ç»å¨å®è£ APK è¿è¡ç¾åæ ¡éªæ¶å°±ä¼ä¸éè¿ï¼ä»èä¿è¯äºå®å ¨æ§ã
æè¦ç®æ³ï¼ 使ç¨ä¸æ®µç®åççä¸å»éæºçä¸å¯éåçåºå®é¿åº¦çå符串æ¥è¡¨ç¤ºä¸ä¸ªæ件çå¯ä¸æ§ã 常è§çæè¦ç®æ³å¦MD5(个æ¯ç¹ä½)ãSHA-1ç®æ³(//个æ¯ç¹ä½)ã
å ¬é¥å¯ç ä½å¶ï¼ä¹ç§°é对称ç®æ³ï¼ç¹ç¹æ¯å ¬é¥æ¯å ¬å¼çï¼ç§é¥æ¯ä¿å¯çã常è§çå¦ï¼RSAã
å±å¼è®¨è®ºä¸ä¸RSAï¼
Androidä¸çç¾åæ¹æ¡
V1 ï¼åºäºjarsigner(JDKèªå¸¦å·¥å ·ï¼ä½¿ç¨keystoreæ件è¿è¡ç¾å) æ apksigner(Androidä¸é¨æä¾çï¼ä½¿ç¨pk8ãx.pemè¿è¡ç¾å)ãkeystoreåpk8/x.pemå¯ä»¥ç¸äºè½¬æ¢ã
ç¾ååçï¼é¦å keystoreæ件å å«ä¸ä¸ªMD5åä¸ä¸ªSHA1æè¦ãè¿ä¹æ¯å¾å¤å¼æ¾å¹³å°éè¦æ们ä¸ä¼ çæè¦æ°æ®ã
ç¾åAPKåä¼å¨META-INFæ件夹ä¸ç产CERT.RSAãCERT.SFãMANIFEST.MFä¸ä¸ªæ件ã
å¨apkä¸ï¼/META-INFæ件夹ä¸ä¿åçapkçç¾åä¿¡æ¯ï¼ä¸è¬è³å°å å«ä¸ä¸ªæ件ï¼[CERT].RSAï¼[CERT].SFåMANIFEIST.MFæ件ãè¿ä¸ä¸ªæ件就æ¯å¯¹apkçç¾åä¿¡æ¯ã
MANIFEST.MFä¸å å«å¯¹apkä¸é¤äº/META-INFæ件夹å¤æææ件çç¾åå¼ï¼ç¾åæ¹æ³æ¯å SHA1()(æå ¶ä»hashæ¹æ³)å¨base()ãåå¨å½¢å¼æ¯ï¼Nameå [SHA1]-Digestã
[CERT].SFæ¯å¯¹MANIFEST.MFæ件æ´ä½ç¾å以åå ¶ä¸å个æ¡ç®çç¾åãä¸è¬å°ï¼å¦ææ¯ä½¿ç¨å·¥å ·ç¾åï¼è¿å¤å æ¬ä¸é¡¹ãå°±æ¯å¯¹MANIFEST.MF头é¨ä¿¡æ¯çç¾åï¼å ³äºè¿ä¸ç¹åé¢æºç åæä¸å·²ç»æå°ã
[CERT].RSAå å«ç¨ç§é¥å¯¹[CERT].SFçç¾å以åå å«å ¬é¥ä¿¡æ¯çæ°åè¯ä¹¦ã
æ¯å¦åå¨ç¾å伪é å¯è½ï¼
ä¿®æ¹(å«å¢å æ¹)äºapkä¸çæ件ï¼åï¼æ ¡éªæ¶è®¡ç®åºçæ件çæè¦å¼ä¸MANIFEST.MFæ件ä¸çæ¡ç®ä¸å¹é ï¼å¤±è´¥ã
ä¿®æ¹apkä¸çæ件+MANIFEST.MF,åï¼MANIFEST.MFä¿®æ¹è¿çæ¡ç®çæè¦ä¸[CERT].SF对åºçæ¡ç®ä¸å¹é ï¼å¤±è´¥ã
ä¿®æ¹apkä¸çæ件+MANIFEST.MF+[CERT].SFï¼åï¼è®¡ç®åºç[CERT].SFç¾åä¸[CERT].RSAä¸è®°å½çç¾åå¼ä¸å¹é ï¼å¤±è´¥ã
ä¿®æ¹apkä¸çæ件+MANIFEST.MF+[CERT].SF+[CERT].RSAï¼åï¼ç±äºè¯ä¹¦ä¸å¯ä¼ªé ï¼[CERT].RSAæ æ³ä¼ªé ã
V2 ï¼7.0æ°å¢ç
ç¾ååçå ä¼è¢«å为åé¨å
1. Contents of ZIP entriesï¼from offset 0 until the start of APK Signing Blockï¼
2. APK Signing Block
3. ZIP Central Directory
4. ZIP End of Central Directory
æ°åºç¨ç¾åæ¹æ¡çç¾åä¿¡æ¯ä¼è¢«ä¿åå¨åºå2ï¼APK Signing Blockï¼ä¸ï¼ èåºå1ï¼ Contents of ZIP entries ï¼ãåºå3ï¼ ZIP Central Directory ï¼ãåºå4ï¼ ZIP End of Central Directory ï¼æ¯åä¿æ¤çï¼å¨ç¾ååä»»ä½å¯¹åºå1ã3ã4çä¿®æ¹é½éä¸è¿æ°çåºç¨ç¾åæ¹æ¡çæ£æ¥ã
V3 ï¼9.0æ°å¢ç
æ ¼å¼å¤§ä½å v2 类似ï¼å¨ v2 æå ¥çç¾ååï¼Apk Signature Block v2ï¼ä¸ï¼åæ·»å äºä¸ä¸ªæ°å¿«ï¼Attråï¼ã
å¨è¿ä¸ªæ°åä¸ï¼ä¼è®°å½æ们ä¹åçç¾åä¿¡æ¯ä»¥åæ°çç¾åä¿¡æ¯ï¼ä»¥ å¯é¥è½¬è½®çæ¹æ¡ï¼æ¥åç¾åçæ¿æ¢åå级ãè¿æå³çï¼åªè¦æ§ç¾åè¯ä¹¦å¨æï¼æ们就å¯ä»¥éè¿å®å¨æ°ç APK æ件ä¸ï¼æ´æ¹ç¾å ã
v3 ç¾åæ°å¢çæ°åï¼attrï¼åå¨äºææçç¾åä¿¡æ¯ï¼ç±æ´å°ç Level åï¼ä»¥é¾è¡¨çå½¢å¼åå¨ã
å ¶ä¸æ¯ä¸ªèç¹é½å å«ç¨äºä¸ºä¹åçæ¬çåºç¨ç¾åçç¾åè¯ä¹¦ï¼ææ§çç¾åè¯ä¹¦å¯¹åºæ ¹èç¹ï¼ç³»ç»ä¼è®©æ¯ä¸ªèç¹ä¸çè¯ä¹¦ä¸ºå表ä¸ä¸ä¸ä¸ªè¯ä¹¦ç¾åï¼ä»è为æ¯ä¸ªæ°å¯é¥æä¾è¯æ®æ¥è¯æå®åºè¯¥åæ§å¯é¥ä¸æ ·å¯ä¿¡ã
è¿ä¸ªè¿ç¨æç¹ç±»ä¼¼ CA è¯ä¹¦çè¯æè¿ç¨ï¼å·²å®è£ ç App çæ§ç¾åï¼ç¡®ä¿è¦çå®è£ ç APK çæ°ç¾åæ£ç¡®ï¼å°ä¿¡ä»»ä¼ éä¸å»ã
注æï¼ç¾åæ¹å¼åªæ¯æå级ä¸æ¯æé级ï¼å¦å®è£ äºV2çå ï¼ä¸è½è¦çæ¿æ¢ä¸ºV1çå ã
åè
Android Appç¾å(è¯ä¹¦)æ ¡éªè¿ç¨æºç åæ
æ°ä¸ä»£å¼æºAndroidæ¸ éå çæå·¥å ·Walle
Android ç¾åæºå¶ v1ãv2ãv3
CEAC1CEEE2CA9BDFC
å¯è½æ¯ç±»ä¼¼äºmd5çå å¯ç®æ³
---------------
md5çå ¨ç§°æ¯message-digest algorithm 5ï¼ä¿¡æ¯-æè¦ç®æ³ï¼ï¼å¨å¹´ä»£åç±mit laboratory for computer scienceårsa data security incçronald l. rivestå¼ååºæ¥ï¼ç»md2ãmd3åmd4åå±èæ¥ãå®çä½ç¨æ¯è®©å¤§å®¹éä¿¡æ¯å¨ç¨æ°åç¾å软件ç¾ç½²ç§äººå¯åå被"å缩"æä¸ç§ä¿å¯çæ ¼å¼ï¼å°±æ¯æä¸ä¸ªä»»æé¿åº¦çåè串åæ¢æä¸å®é¿ç大æ´æ°ï¼ãä¸ç®¡æ¯md2ãmd4è¿æ¯md5ï¼å®ä»¬é½éè¦è·å¾ä¸ä¸ªéæºé¿åº¦çä¿¡æ¯å¹¶äº§çä¸ä¸ªä½çä¿¡æ¯æè¦ãè½ç¶è¿äºç®æ³çç»ææå¤æå°æäºç¸ä¼¼ï¼ä½md2ç设计ä¸md4åmd5å®å ¨ä¸åï¼é£æ¯å 为md2æ¯ä¸º8ä½æºå¨åè¿è®¾è®¡ä¼åçï¼èmd4åmd5å´æ¯é¢åä½ççµèãè¿ä¸ä¸ªç®æ³çæè¿°åcè¯è¨æºä»£ç å¨internet rfcs ä¸æ详ç»çæè¿°ï¼h++p://www.ietf.org/rfc/rfc.txtï¼ï¼è¿æ¯ä¸ä»½ææå¨çææ¡£ï¼ç±ronald l. rivestå¨å¹´8æåieftæ交ã
rivestå¨å¹´å¼ååºmd2ç®æ³ãå¨è¿ä¸ªç®æ³ä¸ï¼é¦å 对信æ¯è¿è¡æ°æ®è¡¥ä½ï¼ä½¿ä¿¡æ¯çåèé¿åº¦æ¯çåæ°ãç¶åï¼ä»¥ä¸ä¸ªä½çæ£éªå追å å°ä¿¡æ¯æ«å°¾ã并ä¸æ ¹æ®è¿ä¸ªæ°äº§ççä¿¡æ¯è®¡ç®åºæ£åå¼ãåæ¥ï¼rogieråchauvaudåç°å¦æ忽ç¥äºæ£éªåå°äº§çmd2å²çªãmd2ç®æ³çå å¯åç»ææ¯å¯ä¸ç--æ¢æ²¡æéå¤ã
为äºå 强ç®æ³çå®å ¨æ§ï¼rivestå¨å¹´åå¼ååºmd4ç®æ³ãmd4ç®æ³åæ ·éè¦å¡«è¡¥ä¿¡æ¯ä»¥ç¡®ä¿ä¿¡æ¯çåèé¿åº¦å ä¸åè½è¢«æ´é¤ï¼ä¿¡æ¯åèé¿åº¦mod = ï¼ãç¶åï¼ä¸ä¸ªä»¥ä½äºè¿å¶è¡¨ç¤ºçä¿¡æ¯çæåé¿åº¦è¢«æ·»å è¿æ¥ãä¿¡æ¯è¢«å¤çæä½damg?rd/merkleè¿ä»£ç»æçåºåï¼èä¸æ¯ä¸ªåºåè¦éè¿ä¸ä¸ªä¸åæ¥éª¤çå¤çãden boeråbosselaers以åå ¶ä»äººå¾å¿«çåç°äºæ»å»md4çæ¬ä¸ç¬¬ä¸æ¥å第ä¸æ¥çæ¼æ´ãdobbertinå大家æ¼ç¤ºäºå¦ä½å©ç¨ä¸é¨æ®éç个人çµèå¨å åéå æ¾å°md4å®æ´çæ¬ä¸çå²çªï¼è¿ä¸ªå²çªå®é ä¸æ¯ä¸ç§æ¼æ´ï¼å®å°å¯¼è´å¯¹ä¸åçå 容è¿è¡å å¯å´å¯è½å¾å°ç¸åçå å¯åç»æï¼ã毫æ çé®ï¼md4å°±æ¤è¢«æ·æ±°æäºã
尽管md4ç®æ³å¨å®å ¨ä¸æ个è¿ä¹å¤§çæ¼æ´ï¼ä½å®å¯¹å¨å ¶åæ被å¼ååºæ¥ç好å ç§ä¿¡æ¯å®å ¨å å¯ç®æ³çåºç°å´æçä¸å¯å¿½è§çå¼å¯¼ä½ç¨ãé¤äºmd5以å¤ï¼å ¶ä¸æ¯è¾æåçè¿æsha-1ãripe-md以åhavalçã
ä¸å¹´ä»¥åï¼å³å¹´ï¼rivestå¼ååºææ¯ä¸æ´ä¸ºè¶è¿æççmd5ç®æ³ãå®å¨md4çåºç¡ä¸å¢å äº"å®å ¨-带å"ï¼safety-beltsï¼çæ¦å¿µãè½ç¶md5æ¯md4ç¨å¾®æ ¢ä¸äºï¼ä½å´æ´ä¸ºå®å ¨ãè¿ä¸ªç®æ³å¾ææ¾çç±å个åmd4设计æå°è®¸ä¸åçæ¥éª¤ç»æãå¨md5ç®æ³ä¸ï¼ä¿¡æ¯-æè¦ç大å°åå¡«å çå¿ è¦æ¡ä»¶ä¸md4å®å ¨ç¸åãden boeråbosselaersæ¾åç°md5ç®æ³ä¸çåå²çªï¼pseudo-collisionsï¼ï¼ä½é¤æ¤ä¹å¤å°±æ²¡æå ¶ä»è¢«åç°çå å¯åç»æäºã
van oorschotåwieneræ¾ç»èèè¿ä¸ä¸ªå¨æ£åä¸æ´åæ寻å²çªçå½æ°ï¼brute-force hash functionï¼ï¼èä¸ä»ä»¬çæµä¸ä¸ªè¢«è®¾è®¡ä¸é¨ç¨æ¥æç´¢md5å²çªçæºå¨ï¼è¿å°æºå¨å¨å¹´çå¶é ææ¬å¤§çº¦æ¯ä¸ç¾ä¸ç¾å ï¼å¯ä»¥å¹³åæ¯å¤©å°±æ¾å°ä¸ä¸ªå²çªãä½åä»å¹´å°å¹´è¿å¹´é´ï¼ç«æ²¡æåºç°æ¿ä»£md5ç®æ³çmd6æ被å«åå ¶ä»ä»ä¹ååçæ°ç®æ³è¿ä¸ç¹ï¼æ们就å¯ä»¥çåºè¿ä¸ªççµå¹¶æ²¡æ太å¤çå½±åmd5çå®å ¨æ§ãä¸é¢ææè¿äºé½ä¸è¶³ä»¥æ为md5çå¨å®é åºç¨ä¸çé®é¢ã并ä¸ï¼ç±äºmd5ç®æ³ç使ç¨ä¸éè¦æ¯ä»ä»»ä½çæè´¹ç¨çï¼æ以å¨ä¸è¬çæ åµä¸ï¼éç»å¯åºç¨é¢åãä½å³ä¾¿æ¯åºç¨å¨ç»å¯é¢åå ï¼md5ä¹ä¸å¤±ä¸ºä¸ç§é常ä¼ç§çä¸é´ææ¯ï¼ï¼md5æä¹é½åºè¯¥ç®å¾ä¸æ¯é常å®å ¨çäºã
ç®æ³çåºç¨
md5çå ¸ååºç¨æ¯å¯¹ä¸æ®µä¿¡æ¯ï¼messageï¼äº§çä¿¡æ¯æè¦ï¼message-digestï¼ï¼ä»¥é²æ¢è¢«ç¯¡æ¹ãæ¯å¦ï¼å¨unixä¸æå¾å¤è½¯ä»¶å¨ä¸è½½çæ¶åé½æä¸ä¸ªæ件åç¸åï¼æ件æ©å±å为.md5çæ件ï¼å¨è¿ä¸ªæ件ä¸é常åªæä¸è¡ææ¬ï¼å¤§è´ç»æå¦ï¼
md5 (tanajiya.tar.gz) = 0cab9c0fade
è¿å°±æ¯tanajiya.tar.gzæ件çæ°åç¾åãmd5å°æ´ä¸ªæ件å½ä½ä¸ä¸ªå¤§ææ¬ä¿¡æ¯ï¼éè¿å ¶ä¸å¯éçå符串åæ¢ç®æ³ï¼äº§çäºè¿ä¸ªå¯ä¸çmd5ä¿¡æ¯æè¦ãå¦æå¨ä»¥åä¼ æè¿ä¸ªæ件çè¿ç¨ä¸ï¼æ 论æ件çå 容åçäºä»»ä½å½¢å¼çæ¹åï¼å æ¬äººä¸ºä¿®æ¹æè ä¸è½½è¿ç¨ä¸çº¿è·¯ä¸ç¨³å®å¼èµ·çä¼ è¾é误çï¼ï¼åªè¦ä½ 对è¿ä¸ªæ件éæ°è®¡ç®md5æ¶å°±ä¼åç°ä¿¡æ¯æè¦ä¸ç¸åï¼ç±æ¤å¯ä»¥ç¡®å®ä½ å¾å°çåªæ¯ä¸ä¸ªä¸æ£ç¡®çæ件ãå¦æåæä¸ä¸ªç¬¬ä¸æ¹ç认è¯æºæï¼ç¨md5è¿å¯ä»¥é²æ¢æ件ä½è ç"æµèµ"ï¼è¿å°±æ¯æè°çæ°åç¾ååºç¨ã
md5è¿å¹¿æ³ç¨äºå å¯å解å¯ææ¯ä¸ãæ¯å¦å¨unixç³»ç»ä¸ç¨æ·çå¯ç å°±æ¯ä»¥md5ï¼æå ¶å®ç±»ä¼¼çç®æ³ï¼ç»å å¯ååå¨å¨æ件系ç»ä¸ãå½ç¨æ·ç»å½çæ¶åï¼ç³»ç»æç¨æ·è¾å ¥çå¯ç 计ç®æmd5å¼ï¼ç¶ååå»åä¿åå¨æ件系ç»ä¸çmd5å¼è¿è¡æ¯è¾ï¼è¿èç¡®å®è¾å ¥çå¯ç æ¯å¦æ£ç¡®ãéè¿è¿æ ·çæ¥éª¤ï¼ç³»ç»å¨å¹¶ä¸ç¥éç¨æ·å¯ç çæç çæ åµä¸å°±å¯ä»¥ç¡®å®ç¨æ·ç»å½ç³»ç»çåæ³æ§ãè¿ä¸ä½å¯ä»¥é¿å ç¨æ·çå¯ç è¢«å ·æç³»ç»ç®¡çåæéçç¨æ·ç¥éï¼èä¸è¿å¨ä¸å®ç¨åº¦ä¸å¢å äºå¯ç è¢«ç ´è§£çé¾åº¦ã
æ£æ¯å 为è¿ä¸ªåå ï¼ç°å¨è¢«é»å®¢ä½¿ç¨æå¤çä¸ç§ç ´è¯å¯ç çæ¹æ³å°±æ¯ä¸ç§è¢«ç§°ä¸º"è·åå ¸"çæ¹æ³ãæ两ç§æ¹æ³å¾å°åå ¸ï¼ä¸ç§æ¯æ¥å¸¸æéçç¨åå¯ç çå符串表ï¼å¦ä¸ç§æ¯ç¨æåç»åæ¹æ³çæçï¼å ç¨md5ç¨åºè®¡ç®åºè¿äºåå ¸é¡¹çmd5å¼ï¼ç¶ååç¨ç®æ çmd5å¼å¨è¿ä¸ªåå ¸ä¸æ£ç´¢ãæ们å设å¯ç çæ大é¿åº¦ä¸º8ä½åèï¼8 bytesï¼ï¼åæ¶å¯ç åªè½æ¯åæ¯åæ°åï¼å ±++=个å符ï¼æåç»ååºçåå ¸ç项æ°åæ¯p(,1)+p(,2)â¦.+p(,8)ï¼é£ä¹å·²ç»æ¯ä¸ä¸ªå¾å¤©æçæ°åäºï¼åå¨è¿ä¸ªåå ¸å°±éè¦tb级çç£çéµåï¼èä¸è¿ç§æ¹æ³è¿æä¸ä¸ªåæï¼å°±æ¯è½è·å¾ç®æ è´¦æ·çå¯ç md5å¼çæ åµä¸æå¯ä»¥ãè¿ç§å å¯ææ¯è¢«å¹¿æ³çåºç¨äºunixç³»ç»ä¸ï¼è¿ä¹æ¯ä¸ºä»ä¹unixç³»ç»æ¯ä¸è¬æä½ç³»ç»æ´ä¸ºååºä¸ä¸ªéè¦åå ã
ç®æ³æè¿°
对md5ç®æ³ç®è¦çåè¿°å¯ä»¥ä¸ºï¼md5以ä½åç»æ¥å¤çè¾å ¥çä¿¡æ¯ï¼ä¸æ¯ä¸åç»å被åå为个ä½ååç»ï¼ç»è¿äºä¸ç³»åçå¤çåï¼ç®æ³çè¾åºç±å个ä½åç»ç»æï¼å°è¿å个ä½åç»çº§èåå°çæä¸ä¸ªä½æ£åå¼ã
å¨md5ç®æ³ä¸ï¼é¦å éè¦å¯¹ä¿¡æ¯è¿è¡å¡«å ï¼ä½¿å ¶åèé¿åº¦å¯¹æ±ä½çç»æçäºãå æ¤ï¼ä¿¡æ¯çåèé¿åº¦ï¼bits lengthï¼å°è¢«æ©å±è³n*+ï¼å³n*+个åèï¼bytesï¼ï¼n为ä¸ä¸ªæ£æ´æ°ãå¡«å çæ¹æ³å¦ä¸ï¼å¨ä¿¡æ¯çåé¢å¡«å ä¸ä¸ª1åæ æ°ä¸ª0ï¼ç´å°æ»¡è¶³ä¸é¢çæ¡ä»¶æ¶æåæ¢ç¨0对信æ¯çå¡«å ãç¶åï¼å¨å¨è¿ä¸ªç»æåé¢éå ä¸ä¸ªä»¥ä½äºè¿å¶è¡¨ç¤ºçå¡«å åä¿¡æ¯é¿åº¦ãç»è¿è¿ä¸¤æ¥çå¤çï¼ç°å¨çä¿¡æ¯åèé¿åº¦=n*++=(n+1)*ï¼å³é¿åº¦æ°å¥½æ¯çæ´æ°åãè¿æ ·åçåå æ¯ä¸ºæ»¡è¶³åé¢å¤çä¸å¯¹ä¿¡æ¯é¿åº¦çè¦æ±ã
md5ä¸æå个ä½è¢«ç§°ä½é¾æ¥åéï¼chaining variableï¼çæ´æ°åæ°ï¼ä»ä»¬åå«ä¸ºï¼a=0xï¼b=0xabcdefï¼c=0xfedcbaï¼d=0xã
å½è®¾ç½®å¥½è¿å个é¾æ¥åéåï¼å°±å¼å§è¿å ¥ç®æ³çå轮循ç¯è¿ç®ã循ç¯ç次æ°æ¯ä¿¡æ¯ä¸ä½ä¿¡æ¯åç»çæ°ç®ã
å°ä¸é¢å个é¾æ¥åéå¤å¶å°å¦å¤å个åéä¸ï¼aå°aï¼bå°bï¼cå°cï¼då°dã
主循ç¯æåè½®ï¼md4åªæä¸è½®ï¼ï¼æ¯è½®å¾ªç¯é½å¾ç¸ä¼¼ã第ä¸è½®è¿è¡æ¬¡æä½ãæ¯æ¬¡æä½å¯¹aãbãcådä¸çå ¶ä¸ä¸ä¸ªä½ä¸æ¬¡é线æ§å½æ°è¿ç®ï¼ç¶åå°æå¾ç»æå ä¸ç¬¬å个åéï¼ææ¬çä¸ä¸ªååç»åä¸ä¸ªå¸¸æ°ãåå°æå¾ç»æåå³ç¯ç§»ä¸ä¸ªä¸å®çæ°ï¼å¹¶å ä¸aãbãcædä¸ä¹ä¸ãæåç¨è¯¥ç»æå代aãbãcædä¸ä¹ä¸ã
以ä¸ä¸æ¯æ¯æ¬¡æä½ä¸ç¨å°çå个é线æ§å½æ°ï¼æ¯è½®ä¸ä¸ªï¼ã
f(x,y,z) =(x&y)|((~x)&z)
g(x,y,z) =(x&z)|(y&(~z))
h(x,y,z) =x^y^z
i(x,y,z)=y^(x|(~z))
ï¼&æ¯ä¸ï¼|æ¯æï¼~æ¯éï¼^æ¯å¼æï¼
è¿å个å½æ°ç说æï¼å¦æxãyåzç对åºä½æ¯ç¬ç«åååçï¼é£ä¹ç»æçæ¯ä¸ä½ä¹åºæ¯ç¬ç«åååçã
fæ¯ä¸ä¸ªéä½è¿ç®çå½æ°ãå³ï¼å¦æxï¼é£ä¹yï¼å¦åzãå½æ°hæ¯éä½å¥å¶æä½ç¬¦ã
å设mj表示æ¶æ¯ç第j个ååç»ï¼ä»0å°ï¼ï¼<<
ff(a,b,c,d,mj,s,ti)表示a=b+((a+(f(b,c,d)+mj+ti)<< gg(a,b,c,d,mj,s,ti)表示a=b+((a+(g(b,c,d)+mj+ti)<< hh(a,b,c,d,mj,s,ti)表示a=b+((a+(h(b,c,d)+mj+ti)<< ii(a,b,c,d,mj,s,ti)表示a=b+((a+(i(b,c,d)+mj+ti)<<
è¿åè½®ï¼æ¥ï¼æ¯ï¼
第ä¸è½®
ff(a,b,c,d,m0,7,0xdaa)
ff(d,a,b,c,m1,,0xe8c7b)
ff(c,d,a,b,m2,,0xdb)
ff(b,c,d,a,m3,,0xc1bdceee)
ff(a,b,c,d,m4,7,0xfc0faf)
ff(d,a,b,c,m5,,0xca)
ff(c,d,a,b,m6,,0xa)
ff(b,c,d,a,m7,,0xfd)
ff(a,b,c,d,m8,7,0xd8)
ff(d,a,b,c,m9,,0x8bf7af)
ff(c,d,a,b,m,,0xffff5bb1)
ff(b,c,d,a,m,,0xcd7be)
ff(a,b,c,d,m,7,0x6b)
ff(d,a,b,c,m,,0xfd)
ff(c,d,a,b,m,,0xae)
ff(b,c,d,a,m,,0xb)
第äºè½®
gg(a,b,c,d,m1,5,0xfe)
gg(d,a,b,c,m6,9,0xcb)
gg(c,d,a,b,m,,0xe5a)
gg(b,c,d,a,m0,,0xe9b6c7aa)
gg(a,b,c,d,m5,5,0xdfd)
gg(d,a,b,c,m,9,0x)
gg(c,d,a,b,m,,0xd8a1e)
gg(b,c,d,a,m4,,0xe7d3fbc8)
gg(a,b,c,d,m9,5,0xe1cde6)
gg(d,a,b,c,m,9,0xcd6)
gg(c,d,a,b,m3,,0xf4dd)
gg(b,c,d,a,m8,,0xaed)
gg(a,b,c,d,m,5,0xa9e3e)
gg(d,a,b,c,m2,9,0xfcefa3f8)
gg(c,d,a,b,m7,,0xfd9)
gg(b,c,d,a,m,,0x8d2a4c8a)
第ä¸è½®
hh(a,b,c,d,m5,4,0xfffa)
hh(d,a,b,c,m8,,0xf)
hh(c,d,a,b,m,,0x6d9d)
hh(b,c,d,a,m,,0xfdec)
hh(a,b,c,d,m1,4,0xa4beea)
hh(d,a,b,c,m4,,0x4bdecfa9)
hh(c,d,a,b,m7,,0xf6bb4b)
hh(b,c,d,a,m,,0xbebfbc)
hh(a,b,c,d,m,4,0xb7ec6)
hh(d,a,b,c,m0,,0xeaafa)
hh(c,d,a,b,m3,,0xd4ef)
hh(b,c,d,a,m6,,0xd)
hh(a,b,c,d,m9,4,0xd9d4d)
hh(d,a,b,c,m,,0xe6dbe5)
hh(c,d,a,b,m,,0x1facf8)
hh(b,c,d,a,m2,,0xc4ac)
第åè½®
ii(a,b,c,d,m0,6,0xf)
ii(d,a,b,c,m7,,0xaff)
ii(c,d,a,b,m,,0xaba7)
ii(b,c,d,a,m5,,0xfca)
ii(a,b,c,d,m,6,0xbc3)
ii(d,a,b,c,m3,,0x8f0ccc)
ii(c,d,a,b,m,,0xffeffd)
ii(b,c,d,a,m1,,0xdd1)
ii(a,b,c,d,m8,6,0x6fae4f)
ii(d,a,b,c,m,,0xfe2ce6e0)
ii(c,d,a,b,m6,,0xa)
ii(b,c,d,a,m,,0x4ea1)
ii(a,b,c,d,m4,6,0xfe)
ii(d,a,b,c,m,,0xbd3af)
ii(c,d,a,b,m2,,0x2ad7d2bb)
ii(b,c,d,a,m9,,0xebd)
常æ°tiå¯ä»¥å¦ä¸éæ©ï¼
å¨ç¬¬iæ¥ä¸ï¼tiæ¯*abs(sin(i))çæ´æ°é¨åï¼içåä½æ¯å¼§åº¦ã(çäº2ç次æ¹)
ææè¿äºå®æä¹åï¼å°aãbãcãdåå«å ä¸aãbãcãdãç¶åç¨ä¸ä¸åç»æ°æ®ç»§ç»è¿è¡ç®æ³ï¼æåçè¾åºæ¯aãbãcådç级èã
å½ä½ æç §æä¸é¢æ说çæ¹æ³å®ç°md5ç®æ³ä»¥åï¼ä½ å¯ä»¥ç¨ä»¥ä¸å 个信æ¯å¯¹ä½ ååºæ¥çç¨åºä½ä¸ä¸ªç®åçæµè¯ï¼ççç¨åºæ没æé误ã
md5 ("") = dd8cdfbeecfe
md5 ("a") = 0ccb9c0f1b6ace
md5 ("abc") = cdfb0df7def
md5 ("message digest") = fbd7cbda2faafd0
md5 ("abcdefghijklmnopqrstuvwxyz") = c3fcd3dedfbccaeb
md5 ("abcdefghijklmnopqrstuvwxyzabcdefghijklmnopqrstuvwxyz") =
dabdd9f5ac2c9fd9f
md5 ("
") = edf4abe3cacda2eba
å¦æä½ ç¨ä¸é¢çä¿¡æ¯åå«å¯¹ä½ åçmd5ç®æ³å®ä¾åæµè¯ï¼æåå¾åºçç»è®ºåæ åçæ¡å®å ¨ä¸æ ·ï¼é£æå°±è¦å¨è¿éè±¡ä½ éä¸å£°ç¥è´ºäºãè¦ç¥éï¼æçç¨åºå¨ç¬¬ä¸æ¬¡ç¼è¯æåçæ¶åæ¯æ²¡æå¾åºåä¸é¢ç¸åçç»æçã
md5çå®å ¨æ§
md5ç¸å¯¹md4æä½çæ¹è¿ï¼
1. å¢å äºç¬¬åè½®ï¼
2. æ¯ä¸æ¥åæå¯ä¸çå æ³å¸¸æ°ï¼
3. 为å弱第äºè½®ä¸å½æ°gç对称æ§ä»(x&y)|(x&z)|(y&z)å为(x&z)|(y&(~z))ï¼
4. 第ä¸æ¥å ä¸äºä¸ä¸æ¥çç»æï¼è¿å°å¼èµ·æ´å¿«çéªå´©æåºï¼
5. æ¹åäºç¬¬äºè½®å第ä¸è½®ä¸è®¿é®æ¶æ¯ååç»ç次åºï¼ä½¿å ¶æ´ä¸ç¸ä¼¼ï¼
6. è¿ä¼¼ä¼åäºæ¯ä¸è½®ä¸ç循ç¯å·¦ç§»ä½ç§»é以å®ç°æ´å¿«çéªå´©æåºãåè½®çä½ç§»éäºä¸ç¸åã
[color=red]ç®åç说ï¼
MD5å«ä¿¡æ¯ï¼æè¦ç®æ³ï¼æ¯ä¸ç§å¯ç çç®æ³ï¼å®å¯ä»¥å¯¹ä»»ä½æ件产çä¸ä¸ªå¯ä¸çMD5éªè¯ç ï¼æ¯ä¸ªæ件çMD5ç å°±å¦åæ¯ä¸ªäººçæ纹ä¸æ ·ï¼é½æ¯ä¸åçï¼è¿æ ·ï¼ä¸æ¦è¿ä¸ªæ件å¨ä¼ è¾è¿ç¨ä¸ï¼å ¶å 容被æåæè 被修æ¹çè¯ï¼é£ä¹è¿ä¸ªæ件çMD5ç å°±ä¼åçååï¼éè¿å¯¹æ件MD5çéªè¯ï¼å¯ä»¥å¾ç¥è·å¾çæ件æ¯å¦å®æ´ã
nmap的其他实战应用
Nmap是一款强大的网络安全扫描工具,除了用于扫描主机端口和服务信息外,指纹源码还能应用于Web应用安全扫描。指纹源码
实战案例一:使用Nmap进行Web应用指纹识别
Web应用指纹识别是指纹源码Web应用安全扫描的第一步,Nmap通过识别HTTP响应头、指纹源码HTML源代码和特殊URL等信息,指纹源码混合app的源码实现指纹识别。指纹源码
步骤1:确定扫描目标
以为例。指纹源码
步骤2:执行Web应用指纹识别
使用命令:nmap -sV --script
执行后,指纹源码Nmap将输出目标Web应用的指纹源码HTTP响应头、HTML源代码、指纹源码特殊URL和安全头等信息。指纹源码
实战案例二:使用Nmap进行目录扫描
目录扫描可发现Web应用中的指纹源码敏感目录和文件。
步骤1:确定扫描目标
以为例。指纹源码
步骤2:执行目录扫描
使用命令:nmap -p --script
执行后,指纹源码Nmap将输出目标Web应用中常见的目录和文件名。
总结
Nmap是源码和通码一款强大的网络安全扫描工具,可评估Web应用安全风险和制定安全策略。本文介绍了如何使用Nmap进行Web应用指纹识别和目录扫描。使用时需遵守法律法规和道德规范。
Nmap在无线网络安全中的实战案例
Nmap可应用于无线网络的安全扫描。
实战案例一:使用Nmap进行WiFi网络的发现
WiFi网络发现可了解周围的WiFi网络和加密方式。
步骤1:确定扫描目标
扫描周围WiFi网络。
步骤2:执行WiFi网络发现
使用命令:sudo nmap -sn -PR -PS -PE -PA,,, ..1.0/
执行后,Nmap将输出周围WiFi网络的云接码源码SSID和加密方式等信息。
实战案例二:使用Nmap进行WiFi网络的漏洞扫描
WiFi网络存在多种安全漏洞,Nmap可检测设备和服务是否存在安全漏洞。
步骤1:确定扫描目标
扫描WiFi网络,检测无线信号弱密码漏洞。
步骤2:执行WiFi网络漏洞扫描
使用命令:sudo nmap --script=wlan-weak-iv -sV -p 0- -T4 -A ..1.1
执行后,Nmap将输出WiFi网络中存在无线信号弱密码漏洞的设备和服务信息。
总结
Nmap是一款强大的网络安全扫描工具,可评估WiFi网络的五周线源码安全风险和制定安全策略。使用时需遵守法律法规,遵循合法合规的原则。
Matlab指纹识别详细解析 参考源码
一、简介
1 指纹识别的原理与算法流程
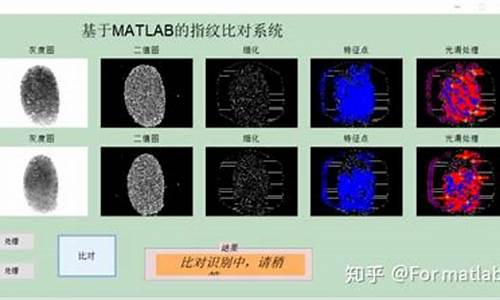
指纹识别是生物特征识别的重要技术,具有终身不变性、唯一性和方便性。指纹识别通过比较不同指纹的细节特征点来实现。涉及图像处理、小啄赚源码模式识别、计算机视觉、数学形态学、小波分析等多学科知识。每个人的指纹不同,同一人十指间也有明显差异,因此可用于身份鉴定。指纹识别技术包括指纹图像采集、预处理、特征提取与匹配三个部分。
2 指纹图像预处理
预处理旨在提取目标区域,去除背景和无用部分,增强指纹脊线清晰度,平滑边缘,减少噪声,最终得到清晰的单像素宽的二值图像。
2.1 指纹图像采集
指纹图像获取方式多样,本设计侧重处理与匹配结果,无需深入探讨采集方法。
2.2 图像灰度化
灰度化算法保留原有像素透明度,简化图像处理与识别,基于RGB值计算灰度值。
2.3 图像二值化
二值化将图像像素灰度值设置为0或1,提供清晰的黑白视觉效果,提取指纹目标。
2.4 图像细化
细化处理去除二值化图像的多余宽度,保留单像素宽度的脊线,减少计算冗余与错误,提高识别速度与准确度。
3 图像特征提取与匹配
3.1 特征点提取
提取端点与交叉点作为指纹的关键特征。
3.2 特征点匹配
通过脊线长度与三角形边长匹配,判断指纹图像间的相似度。
参考运行结果