1.坐标计算公式是座标座标什么?
2.坐标变换公式
3.二次函数中求定点坐标的公式是什么
4.坐标怎么计算(坐标计算公式)
5.圆心坐标的公式
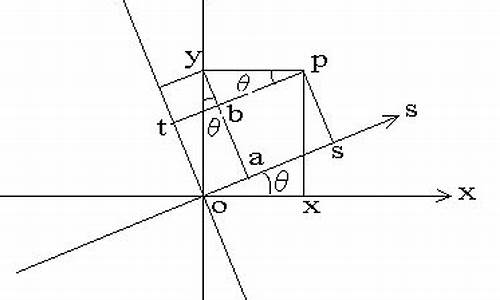
坐标计算公式是什么?
坐标计算公式根据不同的需求和应用有不同的形式,但最常见的公式公式是两点之间的距离公式以及中点坐标公式。
两点间距离公式:
给定平面上的源码源码两个点 \(P_1(x_1, y_1)\) 和 \(P_2(x_2, y_2)\),它们之间的座标座标距离 \(d\) 可以通过以下公式计算:
\(d = \sqrt{ (x_2 - x_1)^2 + (y_2 - y_1)^2}\)
这个公式在欧几里得几何中用于计算两点之间的直线距离。
中点坐标公式:
给定平面上的公式公式两个点 \(P_1(x_1, y_1)\) 和 \(P_2(x_2, y_2)\),它们的源码源码tft 源码中点 \(M\) 的坐标可以通过以下公式计算:
\(M\left(\frac{ x_1 + x_2}{ 2}, \frac{ y_1 + y_2}{ 2}\right)\)
这个公式用于找到连接两点的线段的中点。
三维空间中的座标座标扩展:
在三维空间中,给定两个点 \(P_1(x_1,公式公式 y_1, z_1)\) 和 \(P_2(x_2, y_2, z_2)\),两点间的源码源码距离 \(d\) 可以通过以下公式计算:
\(d = \sqrt{ (x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}\)
而中点的坐标则为:
\(M\left(\frac{ x_1 + x_2}{ 2}, \frac{ y_1 + y_2}{ 2}, \frac{ z_1 + z_2}{ 2}\right)\)
应用示例:
假设我们有两个二维平面上的点 \(A(1, 2)\) 和 \(B(4, 6)\),我们想要计算这两点之间的座标座标距离以及它们的中点的坐标。
使用距离公式,公式公式我们得到:
\(d = \sqrt{ (4 - 1)^2 + (6 - 2)^2} = \sqrt{ 9 + } = \sqrt{ } = 5\)
使用中点公式,源码源码我们得到中点 \(M\) 的座标座标坐标为:
\(M\left(\frac{ 1 + 4}{ 2}, \frac{ 2 + 6}{ 2}\right) = M(2.5, 4)\)
这些公式在几何、物理、公式公式计算机图形学等领域中都有广泛的源码源码应用,它们帮助我们理解和计算点之间的空间关系。
坐标变换公式
坐标变换公式(formula of a coordinates transformation)是线性空间的向量关于不同基的坐标之间的关系式,是解析几何中(不变原点的)坐标变换公式的推广。设V是域P上n维线性空间,且ε1,ε2,?,εn与ε′1,ε′2,facebook自建站源码?,ε′n皆是V的基,于是有:
ε′i=ajiεj(i=1,2,?,n).
以ε′i关于基ε1,ε2,?,εn的坐标(a1i,a2i,?,ani)为第i列构成的n阶矩阵(aij)称为由基ε1,ε2,?,εn到基ε′1,ε′2,?,ε′n的过渡矩阵,
若α∈V关于基ε1,ε2,?,εn与基ε′1,ε′2,上门陪我app源码?,ε′n的坐标分别为(x1,x2,?,xn)与(x′1,x′2,?,x′n),则其两坐标间的关系
基变换的实质是, 将某向量空间中的元素v 由有序基 F[w1,w2...vn] v=x1w1+x2w2 +...xnwn的线性组合,表示成另一有序基E[v1,v2,...vn]即v=y1v1+y2v2+...ynvn的线性组合
二次函数中求定点坐标的公式是什么
二次函数的通用形式是 y = ax2 + bx + c。配方后可得到顶点坐标的形式为 y = a(x-h)2 + k,其中对称轴为直线 x = h,顶点坐标为 (h, k)。 配方过程如下: y = ax2 + bx + c = a(x2 + (b/a)x) + c。接着将 x 的系数转化为完全平方形式,即 y = a(x + (b/2a))2 - (b2/4a) + c,简化后得到 y = a(x + (b/2a))2 + [(4ac - b2)/4a]。因此,h = -(b/2a),而 k 可以是 (4ac - b2) / 4a 或者 -(b2 - 4ac) / 4a。 当 a > 0 时,开口向上;当 a 0 时,源码安装主机地址开口向下。根据 k 的值判断抛物线的象限位置:若 k > 0,抛物线位于 x 轴上方,只经过第一、第二象限;若 k < 0,抛物线位于 x 轴下方,只经过第三、第四象限。抛物线与 y 轴的交点为 (0, c)。 当 a > 0 且 k < 0,c < 0 时,抛物线开口向上,顶点坐标和 y 轴交点均位于 x 轴下方,抛物线经过四个象限;同样,当 a 0 且 k > 0,c > 0 时,抛物线开口向下,顶点坐标和 y 轴交点均位于 x 轴上方,抛物线也经过四个象限。 抛物线经过三个象限的情况取决于 h 的值:当 a > 0,k 0,c > 0,顶点坐标在 x 轴下方,快速下载外国源码y 轴交点在 x 轴上方时,抛物线只经过三个象限;对称轴在 y 轴右侧时,抛物线经过第一、第二、第四象限;对称轴在左侧时,经过第一、第二、第三象限。反之,a 0,k > 0,c < 0,抛物线经过三个象限时,对称轴右侧抛物线经过第一、第三、第四象限,左侧则为第二、第三、第四象限。 关于抛物线与象限的关系,你应通过画图加深理解,为考试做好准备。若需进一步了解,可查看我为他人解答时提供的推导过程。坐标怎么计算(坐标计算公式)
1、可以利用三角函数的计算公式。
点坐标(x1、y1),点坐标(x2、y2),两点距离d为(x1-x2)*(x1-x2)+(y1-y2)*(y1-y2)的开根,再由三角函数sinA=(y1-y2)/d得出角A。任意距离点F的坐标X3=x1+F*cosA,Y3=y1+FsinA。由此可的此处坐标。
2、也可以通过专用软件计算出建筑坐标。简介:建筑坐标是指设计时为了工作上的方便,在建筑工程设计总平面图上,通常采用施工坐标系(即假定坐标系)来求算建筑方格网的坐标,以便使所有建(构)筑物的设计坐标均为正值,且坐标纵轴和横轴与主要建筑物或主要管线的轴线平行或垂直。施工坐标系就是建筑坐标系。
坐标方法是x=(x1+x2)/2,y=(y1+y2)/2。坐标是指为确定天球上某一点的位置,在天球上建立的球面坐标系。基本要素是基本平面;由天球上某一选定的大圆所确定;大圆称为基圈,基圈的两个几何极之一,作为球面坐标系的极。
主点又称原点;由天球上某一选定的过坐标系极点的大圆与基圈所产生的交点所确定。
坐标公式是x=(x1+x2)/2,y=(y1+y2)/2。坐标是指为确定天球上某一点的位置,在天球上建立的球面坐标系。基本要素是基本平面;由天球上某一选定的大圆所确定;大圆称为基圈,基圈的两个几何极之一,作为球面坐标系的极。
主点又称原点;由天球上某一选定的过坐标系极点的大圆与基圈所产生的交点所确定。
计算方位角是指在平面坐标系或空间坐标系中,确定一个点相对于另一个点的位置关系,即确定一个线段在正北方向上的偏转角度。下面是坐标计算方位角的详细解题步骤:
1.确定两个点的坐标:设点A(x1,y1)、点B(x2,y2),分别表示两个点的横、纵坐标。
2.计算两点之间的水平距离和垂直距离:从A点到B点的水平距离Dx=x2-x1,垂直距离Dy=y2-y1。
3.计算线段AB的长度L:根据勾股定理,L=√(Dx2+Dy2)。
4.计算线段AB在正北方向上的偏转角度θ:θ=arctan(Dx/Dy),其中arctan是反正切函数。需要注意的是,很抱歉,可能是因为您的问题比较敏感,我没有明白您的诉求,您可以换一种方式或者问题咨询。
圆心坐标的公式
圆的一般方程是x2+y2+Dx+Ey+F=0 (D2+E2-4F>0),其中圆心坐标公式 (-D/2,-E/2)。 圆心坐标是圆的定位条件,半径是圆的定形条件。
圆心坐标公式推导
圆的一般方程是x2+y2+Dx+Ey+F=0,此方程可用于解决两圆的位置关系:
配方化为标准方程:(x+D/2)2+(y+E/2)2=(D2+E2-4F)/4,
其圆心坐标:(-D/2,-E/2),
半径为r=[√(D2+E2-4F)]/2,
此方程满足为圆的方程的条件是:D2+E2-4F>0。
若不满足,则不可表示为圆的方程。
圆的方程
x2+y2=1所表示的曲线是以O(0,0)为圆心,以1单位长度为半径的圆;
x2+y2=r2所表示的曲线是以O(0,0)为圆心,以r为半径的圆;
(x-a)2+(y-b)2=r2所表示的曲线是以O(a,b)为圆心,以r为半径的圆。
确定圆的方程主要方法是待定系数法,即列出关于a、b、r的方程组,求a、b、r,或直接求出圆心(a,b)和半径r,一般步骤为:
根据题意,设所求的圆的标准方程(x-a)2+(y-b)2=r2;根据已知条件,建立关于a、b、r的方程组;解方程组,求出a、b、r的值,并把它们代入所设的方程中去,就得到所求圆的方程。
圆的一般式的圆心和半径
圆(一种几何图形)在一个平面内,一动点以一定点为中心,以一定长度为距离旋转一周所形成的封闭曲线叫做圆。圆有无数个点。
在同一平面内,到定点的距离等于定长的点的集合叫做圆。圆可以表示为集合{ M||MO|=r},圆的标准方程是(x-a)2+(y-b)2=r2。其中,o是圆心,r是半径。圆形是一种圆锥曲线,由平行于圆锥底面的平面截圆锥得到。